Der Mast und ein alter Grieche
Wie ermittelt man die Kantenlänge um aus einem Quadrat ein gleichmäßiges Achteck zu machen?
Um dem Mast bzw. die Spieren zu runden wird der Querschnitt zunächst als Quadrat gefertigt dessen Kanten dann immer wieder halbiert werden so das irgendwann nur noch kleine Kanten überstehen, der ursprüngliche Balken allmählich immer runder wird, und nach dem glätten mit Schleifpapier zu einem Mast mutiert. So jedenfalls die Theorie.
Der Durchmesser des Mastes hat an seiner breitesten Stelle 56 mm und damit hat auch die Kantenlänge des Quadrates zunächst 56 mm. Das war klar. Aber davon die Hälfte in der 45° Schräge? Pff.
Eine kleine Skizze und der rechte Winkel des Pythagoras, der sein Wort hielt, half.
Mittels der steinalten Erkenntnis a² + b² = c² konnte ich die Diagonale des Quadrates ermitteln wovon ich den Durchmesser des Kreises(Kantenlänge)abzog. Den Rest halbierte ich und schon hatte ich die Hälfte der a² und b² Größe der künftigen Kantenlänge.
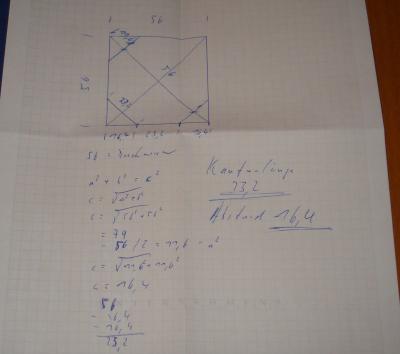
Die gleiche Rechnung noch mal und ich hatte mit der Diagonalen c² den Abstand der neuen Kantenlänge von Aussen um ihn mit dem Streichmass anzuzeichnen. 16,4 mm von Rechts und von Links ergibt schöne gleichmäßige 8 Seiten von 23,2 in der Mitte.
Ohh ja ich weiss es gibt Leute die rechnen was mit Sinus und Kosinus oder so aber das lässt sich zeichnerisch nicht so schön nachvollziehen und zu überprüfen ob es denn auch passt. Der Mast soll ja rund werden und nicht oval gell?
Um dem Mast bzw. die Spieren zu runden wird der Querschnitt zunächst als Quadrat gefertigt dessen Kanten dann immer wieder halbiert werden so das irgendwann nur noch kleine Kanten überstehen, der ursprüngliche Balken allmählich immer runder wird, und nach dem glätten mit Schleifpapier zu einem Mast mutiert. So jedenfalls die Theorie.
Der Durchmesser des Mastes hat an seiner breitesten Stelle 56 mm und damit hat auch die Kantenlänge des Quadrates zunächst 56 mm. Das war klar. Aber davon die Hälfte in der 45° Schräge? Pff.
Eine kleine Skizze und der rechte Winkel des Pythagoras, der sein Wort hielt, half.
Mittels der steinalten Erkenntnis a² + b² = c² konnte ich die Diagonale des Quadrates ermitteln wovon ich den Durchmesser des Kreises(Kantenlänge)abzog. Den Rest halbierte ich und schon hatte ich die Hälfte der a² und b² Größe der künftigen Kantenlänge.

Die gleiche Rechnung noch mal und ich hatte mit der Diagonalen c² den Abstand der neuen Kantenlänge von Aussen um ihn mit dem Streichmass anzuzeichnen. 16,4 mm von Rechts und von Links ergibt schöne gleichmäßige 8 Seiten von 23,2 in der Mitte.
Ohh ja ich weiss es gibt Leute die rechnen was mit Sinus und Kosinus oder so aber das lässt sich zeichnerisch nicht so schön nachvollziehen und zu überprüfen ob es denn auch passt. Der Mast soll ja rund werden und nicht oval gell?
Stockfisch - 7. Jan, 22:57, verfasst in Mast und Spieren